平衡二叉树
二叉排序树很好的平衡了插入与查找的效率,但不平衡的二叉排序树效率大打折扣。今天介绍的AVL树就是一种解决此问题的方案。
定义
平衡二叉树,是一种二叉排序树,其中每一个节点的左子树和右子树的高度差至多等于1。它是一种高度平衡的二叉排序树。意思是说,要么它是一棵空树,要么它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。我们将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF (Balance Factor),那么平衡二叉树上所有结点的平衡因子只可能是-1、0和1。
如下图就不是一棵AVL树,因为结点18的左子树高度为2,右子树高度为0,高度差大于1。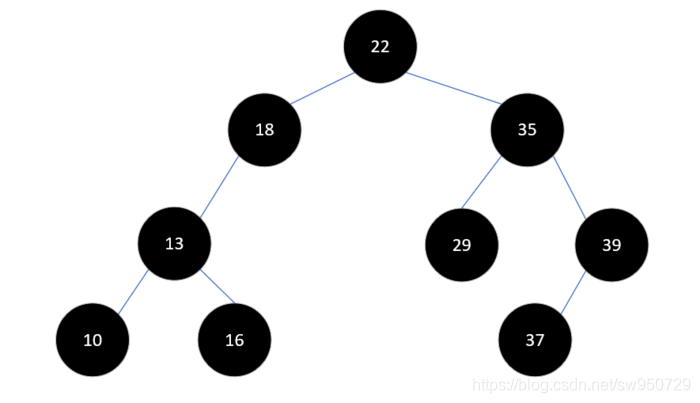
但通过一定的步骤调整之后,可以将其转为一棵平衡二叉树,如下图: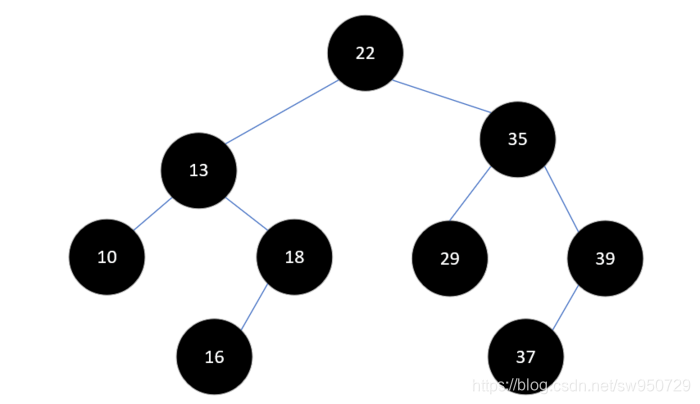
实现原理
平衡二叉树构建的基本思想就是在构建二叉排序树的过程中,每当插入一个结点时,先检查是否因插入而破坏了树的平衡性,若是,则找出最小不平衡子树。在保持二叉排序树特性的前提下,调整最小不平衡子树中各结点之间的链接关系,进行相应的旋转,使之成为新的平衡子树。最小不平衡子树是指距离插入结点最近的,且平衡因子的绝对值大于1 的结点为根的子树。
下面通过一个实例,了解平衡二叉树的构建过程。
假如我们要将数组int[] a = {3, 2, 1, 4, 5, 6, 7, 10, 9, 8}构建成一棵二叉排序树,如果直接按照二叉排序树的定义,会得到下面的结果: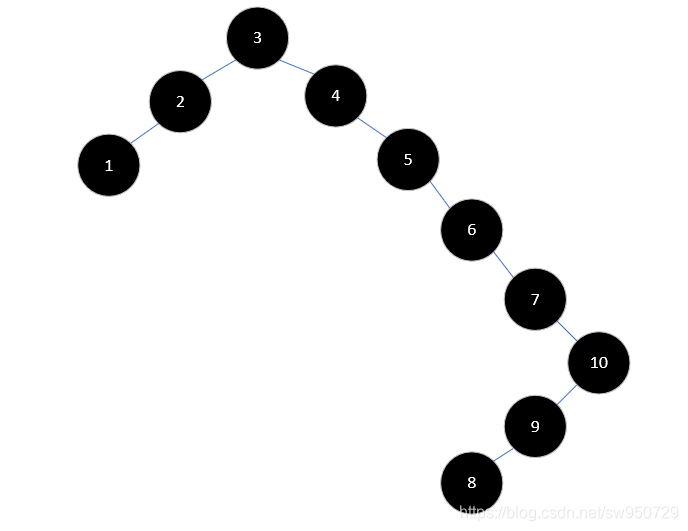
这样的结果对查找是十分不利的,树的高度达到了8,而且大多数只有一个孩子。所以我们需要一些操作,将它变成一棵AVL树。
首先,插入元素3和2时,没有什么影响,此时3的平衡因子为1,2的平衡因子为0,结果如下: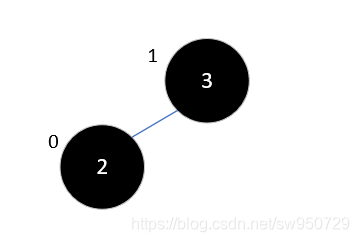
现在,要把1插入树中,这时结果如下所示:
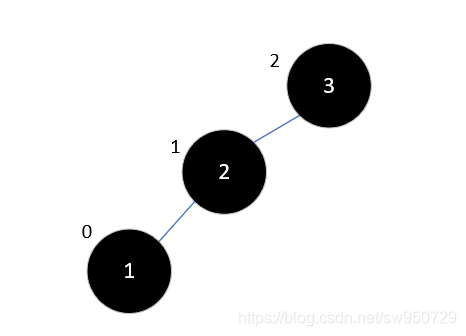
此时3的平衡因子为2了,不再符合平衡二叉树的规则。此时,整棵树就是最小不平衡子树,我们将其右旋:
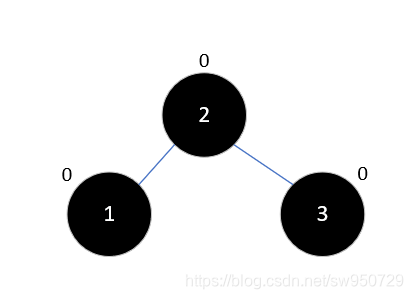
再插入4,也不会影响平衡,结果如下:
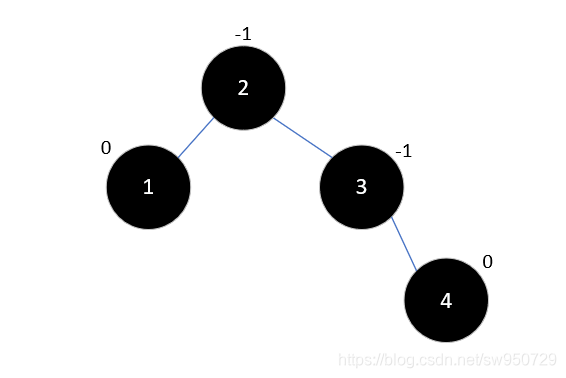
此时,插入元素5,以3为根结点的子树成为了最小不平衡子树,如下所示:
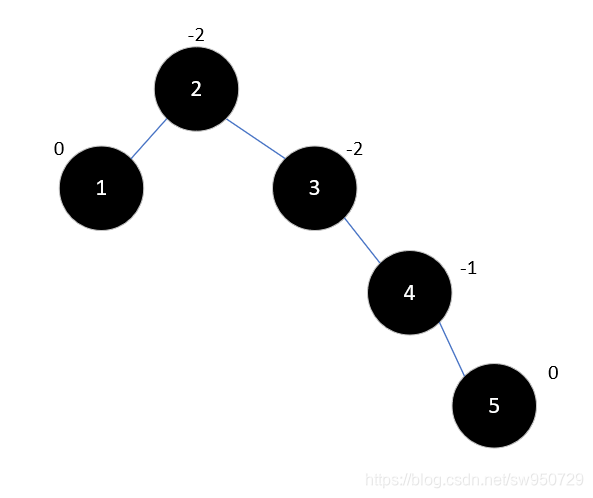
现在要对其进行左旋:
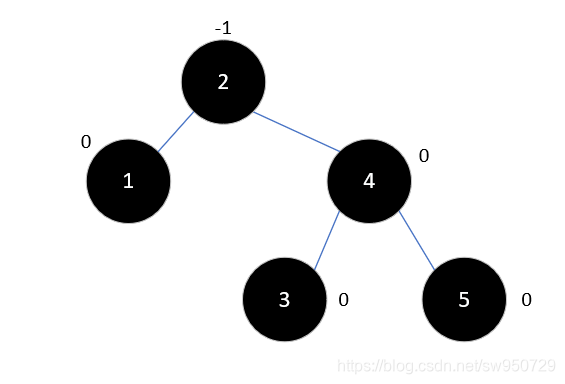
现在继续插入元素6,此时以2为根结点的右子树为最小不平衡子树,结果如下:
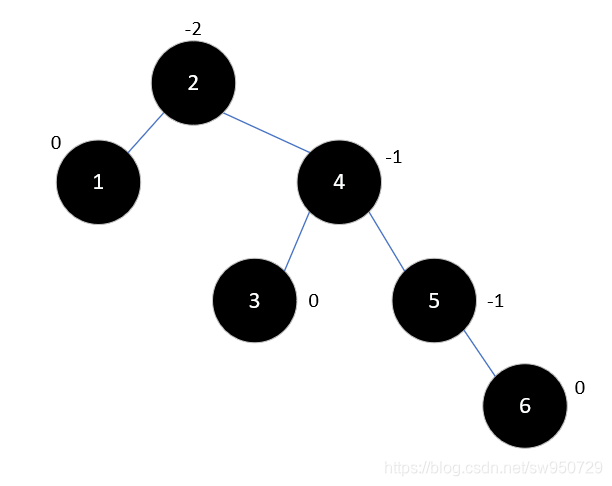
这时再次需要对其进行左旋,这次旋转后要将4的左孩子变为2的右孩子,以满足二叉排序树的定义,如下所示:
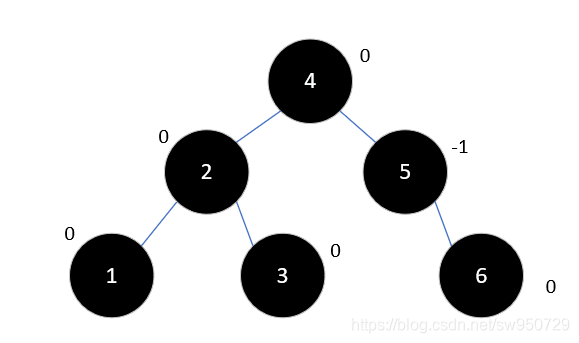
再插入7时,情况和之前有些类似了,结果如下:
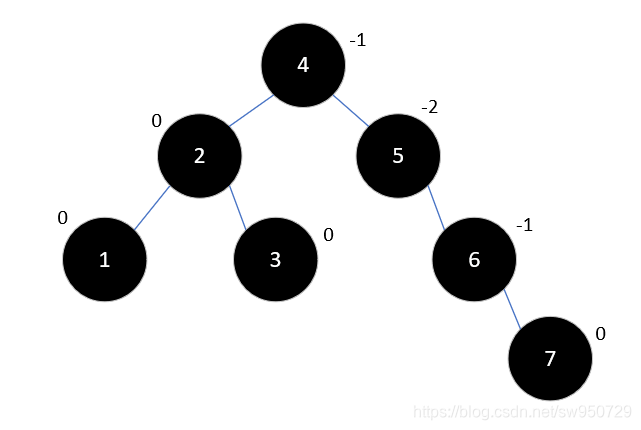
左旋后结果如下:
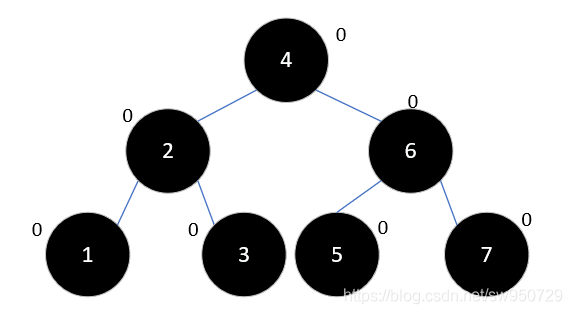
现在,继续插入10,此时无需调整,结果如下:
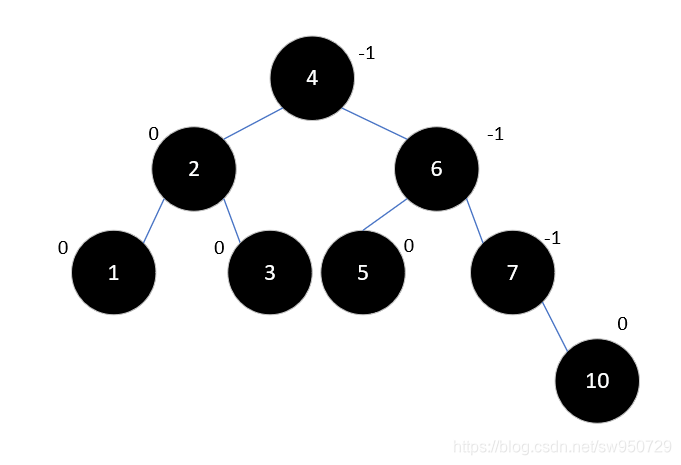
下一步,插入元素9,此时结果如下:
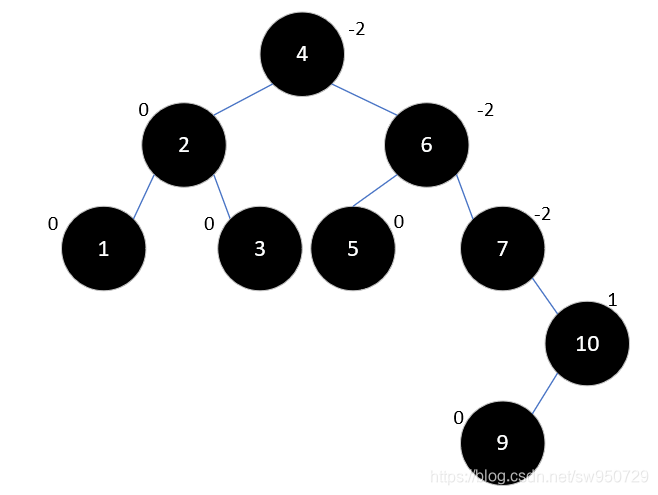
按照之前的经验,这时我们应该进行左旋了,但是左旋之后9将变为10的右孩子,这会不符合二叉排序树的定义。和之前不同的是,7和10的平衡因子符号相反,这是造成这一结果的原因。这种情况下,要先以10为根节点右旋,再进行左旋,结果如下所示:
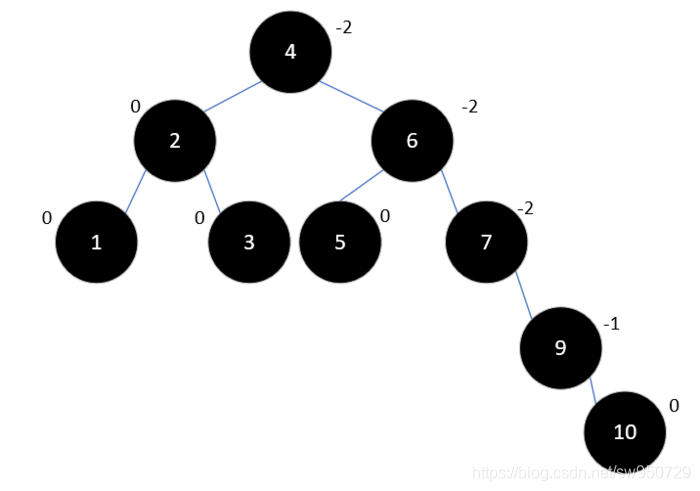
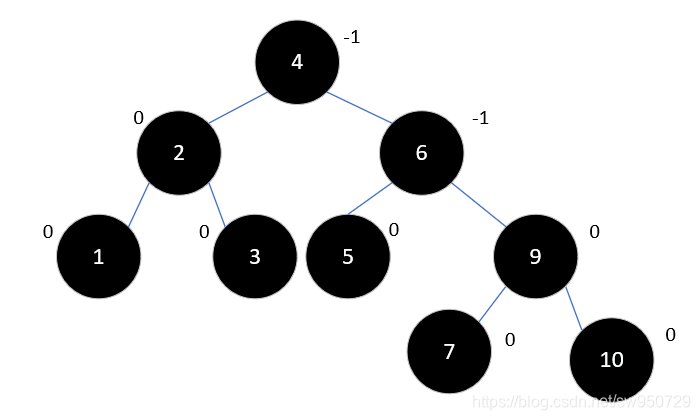
最后插入元素8,如下所示:
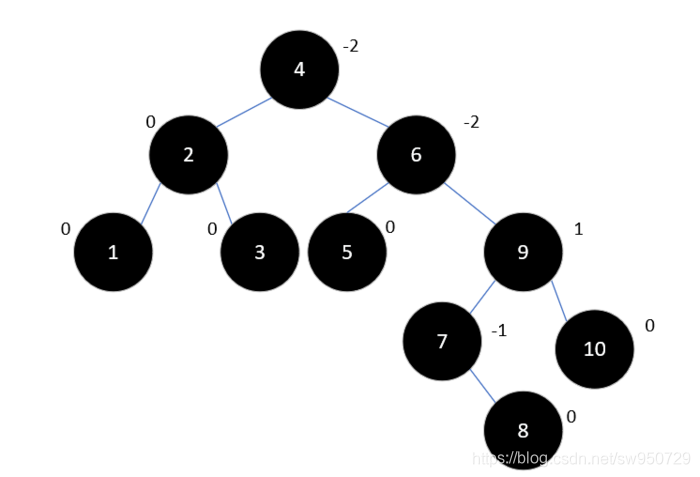
此时情况和上述类似,6是最小不平衡子树的根结点,9和6的平衡因子符号相反,所以先以9为根结点右旋:
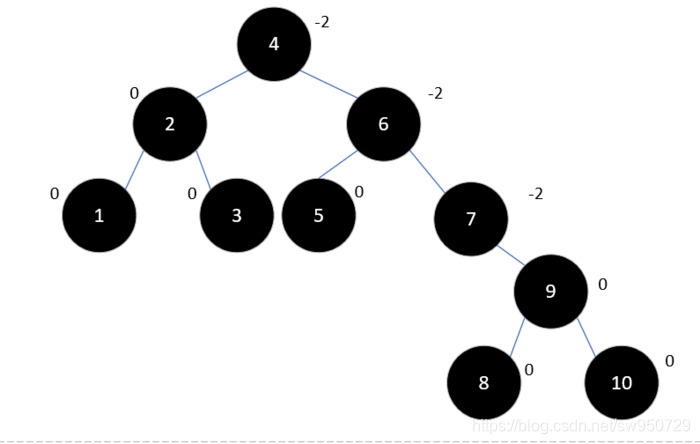
然后再以6左旋:
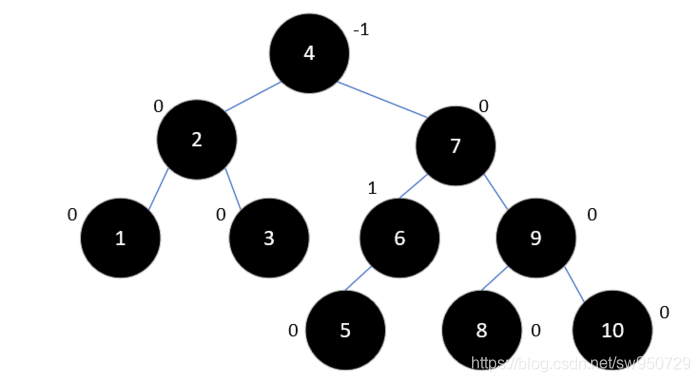
可以看到,此树的高度仅为4,与之前的8相差很多,性能自然也好很多。
平衡二叉树的删除操作与插入类似,这里将不再介绍。大家可以自己思考如何最高效地删除元素,可以分叶结点、仅有一个子结点和有两个子结点三种情况考虑,这里还用到了递归的思想。
接下来我们将介绍另一种实现方式,红黑树。






