TreeMap源码分析

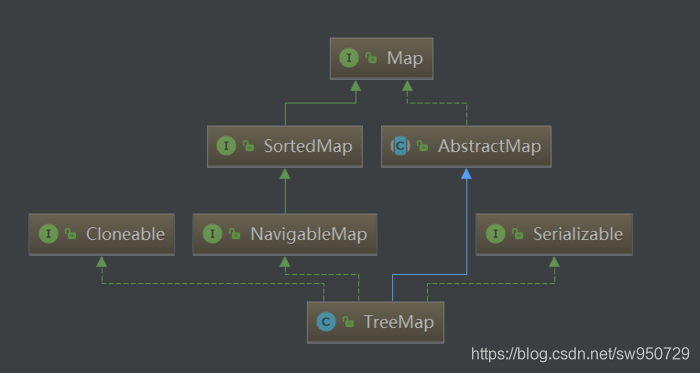
概述

TreeMap是红黑树的java实现，红黑树能保证增、删、查等基本操作的时间复杂度为O(lgN)。
首先我们来看一张TreeMap的继承体系图：

还是比较直观的，这里来简单说一下继承体系中不常见的接口NavigableMap和SortedMap，这两个接口见名知意。先说NavigableMap接口，NavigableMap接口声明了一些列具有导航功能的方法，比如：

/**
 * 返回红黑树中最小键所对应的 Entry
 */
Map.Entry<K,V> firstEntry();

/**
 * 返回最大的键 maxKey，且 maxKey 仅小于参数 key
 */
K lowerKey(K key);

/**
 * 返回最小的键 minKey，且 minKey 仅大于参数 key
 */
K higherKey(K key);

// 其他略

通过这些导航方法，我们可以快速定位到目标的 key 或 Entry。至于 SortedMap 接口，这个接口提供了一些基于有序键的操作，比如:

/**
 * 返回包含键值在 [minKey, toKey) 范围内的 Map
 */
SortedMap<K,V> headMap(K toKey);();

/**
 * 返回包含键值在 [fromKey, toKey) 范围内的 Map
 */
SortedMap<K,V> subMap(K fromKey, K toKey);

// 其他略

以上就是两个接口的介绍，很简单。关于TreeMap的继承体系就这里就说到这，接下来我们深入源码进行分析。

源码分析

添加

红黑树最复杂的无非就是增删了，这边我们先介绍增加一个元素，了解红黑树的都知道，当往 TreeMap 中放入新的键值对后，可能会破坏红黑树的性质。首先我们先巩固一下红黑树的特性。

• 节点是红色或黑色。

• 根节点是黑色。

• 每个叶子节点都是黑色的空节点（NIL节点）。

• 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)。

• 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

接下来我们看看添加到底做了什么处理：

public V put(K key, V value) {
    TreeMapEntry<K,V> t = root;
    if (t == null) {
      
        if (comparator != null) {
            if (key == null) {
                comparator.compare(key, key);
            }
        } else {
            if (key == null) {
                throw new NullPointerException("key == null");
            } else if (!(key instanceof Comparable)) {
                throw new ClassCastException(
                        "Cannot cast" + key.getClass().getName() + " to Comparable.");
            }
        }
        root = new TreeMapEntry<>(key, value, null);
        size = 1;
        modCount++;
        return null;
    }
    int cmp;
    TreeMapEntry<K,V> parent;
    Comparator<? super K> cpr = comparator;
    if (cpr != null) {
        do {
            parent = t;
            cmp = cpr.compare(key, t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    else {
        if (key == null)
            throw new NullPointerException();
        @SuppressWarnings("unchecked")
            Comparable<? super K> k = (Comparable<? super K>) key;
        do {
            parent = t;
            cmp = k.compareTo(t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    TreeMapEntry<K,V> e = new TreeMapEntry<>(key, value, parent);
    if (cmp < 0)
        parent.left = e;
    else
        parent.right = e;
    fixAfterInsertion(e);
    size++;
    modCount++;
    return null;
}

这边会先把根节点暂存依赖，如果根节点为null，则讲新增的这个节点设为根节点。 如果初始化的时候指定了comparator比较器，则讲其插入到指定位置，否则使用key进行比较并且插入。不断的进行比较，找到没有子节点的节点，将其插入到相应节点。(注：如果查找出有相同的值只会更新当前值，cmp小于0是没有左节点，反之没有右节点。)

新插入的树破环的红黑树规则，我们会通过fixAfterInsertion去进行相应的调整，这也是TreeMap插入实现的重点，具体我们看看他是怎么通过java实现的。

    private void fixAfterInsertion(TreeMapEntry<K,V> x) {
        x.color = RED;

        while (x != null && x != root && x.parent.color == RED) {
            if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
                TreeMapEntry<K,V> y = rightOf(parentOf(parentOf(x)));
                if (colorOf(y) == RED) {
                    setColor(parentOf(x), BLACK);
                    setColor(y, BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    x = parentOf(parentOf(x));
                } else {
                    if (x == rightOf(parentOf(x))) {
                        x = parentOf(x);
                        rotateLeft(x);
                    }
                    setColor(parentOf(x), BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    rotateRight(parentOf(parentOf(x)));
                }
            } else {
                TreeMapEntry<K,V> y = leftOf(parentOf(parentOf(x)));
                if (colorOf(y) == RED) {
                    setColor(parentOf(x), BLACK);
                    setColor(y, BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    x = parentOf(parentOf(x));
                } else {
                    if (x == leftOf(parentOf(x))) {
                        x = parentOf(x);
                        rotateRight(x);
                    }
                    setColor(parentOf(x), BLACK);
                    setColor(parentOf(parentOf(x)), RED);
                    rotateLeft(parentOf(parentOf(x)));
                }
            }
        }
        root.color = BLACK;
    }
```  
前方高能。如果不清楚红黑树的特性，建议先去了解红黑树的特性。  

首先将新插入的节点设置为红色，这边做了一个判断，新节点不为null，新节点不为根节点并且新节点的父节点为红色。才会进入内部的判断，因为其本身就是一个红黑树。如果新节点的父节点为黑色，则他依旧满足红黑树的特性。所以当其父节点为红色进入内部的判断。  

如果新节点是其祖父节点的左子孙，则拿到其祖父节点的右儿子，也就是新节点的叔叔。如果叔叔节点是红色。则将其父节点设为黑色，讲叔父节点设为黑色，然后讲新节点直接其祖父节点。

否则如果新节点是其父节点的右节点，以其父节点进行左转，将父节点设为黑色，祖父节点设为红色，在通过祖父节点进行右转。

else内容和上述基本一致。自己分析~~

最后我们还需要将跟节点设为黑色。  

我们稍微看一下，他是怎么进行左转和右转的。  

```java
// 右旋与左旋思路一致，只分析其一
// 结果相当于把p和p的儿子调换了
private void rotateLeft(Entry<K,V> p) {
    if (p != null) {
        // 取出p的右儿子
        Entry<K,V> r = p.right;
        // 然后将p的右儿子的左儿子，也就是p的左孙子变成p的右儿子
        p.right = r.left;
        if (r.left != null)
            // p的左孙子的父亲现在是p
            r.left.parent = p;

        // 然后把p的父亲，设置为p右儿子的父亲
        r.parent = p.parent;
        // 这说明p原来是root节点
        if (p.parent == null)
            root = r;
        else if (p.parent.left == p)
            p.parent.left = r;
        else
            p.parent.right = r;
        r.left = p;
        p.parent = r;
    }
}

//和左旋类似
private void rotateRight(Entry<K,V> p) {
    // ...
}

删除

除了添加操作，红黑树的删除也是很麻烦的…我们看看怎么通过java去实现红黑树的删除。具体代码如下：

public V remove(Object key) {
      TreeMapEntry<K,V> p = getEntry(key);
      if (p == null)
          return null;

      V oldValue = p.value;
      deleteEntry(p);
      return oldValue;
  }

其内部是通过deleteEntry去进行删除的。所以我们具体看看deleteEntry的实现。

private void deleteEntry(TreeMapEntry<K,V> p) {
       modCount++;
       size--;

       if (p.left != null && p.right != null) {
           TreeMapEntry<K,V> s = successor(p);
           p.key = s.key;
           p.value = s.value;
           p = s;
       } 
       
       TreeMapEntry<K,V> replacement = (p.left != null ? p.left : p.right);

       if (replacement != null) {
           // Link replacement to parent
           replacement.parent = p.parent;
           if (p.parent == null)
               root = replacement;
           else if (p == p.parent.left)
               p.parent.left  = replacement;
           else
               p.parent.right = replacement;

           p.left = p.right = p.parent = null;

           // Fix replacement
           if (p.color == BLACK)
               fixAfterDeletion(replacement);
       } else if (p.parent == null) { 
           root = null;
       } else {
           if (p.color == BLACK)
               fixAfterDeletion(p);

           if (p.parent != null) {
               if (p == p.parent.left)
                   p.parent.left = null;
               else if (p == p.parent.right)
                   p.parent.right = null;
               p.parent = null;
           }
       }
   }

根据上述代码，我们可以看出，如果 p 有两个孩子节点，则找到后继节点，并把后继节点的值复制到节点 P 中，并让 p 指向其后继节点。 然后将 replacement parent 引用指向新的父节点，同时让新的父节点指向 replacement。

然后判断如果删除的节点 p 是黑色节点，则需要进行调整。删除的是根结点并且树中只有一个节点，我们将根结点置为null，否则，如果删除的节点没有子节点并且是黑色，则需要调整。最后将p从树中移除。

删除了一个元素，为了保证还是一个红黑树，我们需要将其进行调整，具体代码如下：

  /** From CLR */
    private void fixAfterDeletion(TreeMapEntry<K,V> x) {
        while (x != root && colorOf(x) == BLACK) {
            if (x == leftOf(parentOf(x))) {
                TreeMapEntry<K,V> sib = rightOf(parentOf(x));

                if (colorOf(sib) == RED) {
                    setColor(sib, BLACK);
                    setColor(parentOf(x), RED);
                    rotateLeft(parentOf(x));
                    sib = rightOf(parentOf(x));
                }

                if (colorOf(leftOf(sib))  == BLACK &&
                    colorOf(rightOf(sib)) == BLACK) {
                    setColor(sib, RED);
                    x = parentOf(x);
                } else {
                    if (colorOf(rightOf(sib)) == BLACK) {
                        setColor(leftOf(sib), BLACK);
                        setColor(sib, RED);
                        rotateRight(sib);
                        sib = rightOf(parentOf(x));
                    }
                    setColor(sib, colorOf(parentOf(x)));
                    setColor(parentOf(x), BLACK);
                    setColor(rightOf(sib), BLACK);
                    rotateLeft(parentOf(x));
                    x = root;
                }
            } else { // symmetric
                TreeMapEntry<K,V> sib = leftOf(parentOf(x));

                if (colorOf(sib) == RED) {
                    setColor(sib, BLACK);
                    setColor(parentOf(x), RED);
                    rotateRight(parentOf(x));
                    sib = leftOf(parentOf(x));
                }

                if (colorOf(rightOf(sib)) == BLACK &&
                    colorOf(leftOf(sib)) == BLACK) {
                    setColor(sib, RED);
                    x = parentOf(x);
                } else {
                    if (colorOf(leftOf(sib)) == BLACK) {
                        setColor(rightOf(sib), BLACK);
                        setColor(sib, RED);
                        rotateLeft(sib);
                        sib = leftOf(parentOf(x));
                    }
                    setColor(sib, colorOf(parentOf(x)));
                    setColor(parentOf(x), BLACK);
                    setColor(leftOf(sib), BLACK);
                    rotateRight(parentOf(x));
                    x = root;
                }
            }
        }

        setColor(x, BLACK);
}

如果替换节点是父节点的左节点，并且替换节点的兄弟节点是红色，那我们需要将兄弟节点变成黑色，将父节点变成红色，并且通过父节点进行左旋转，然后将父节点的右节点设为兄弟节点。

如果兄弟节点的左右节点都是黑色的，那么将兄弟节点置为红色，并且将当前节点指向父节点。若兄弟节点的右节点是黑色，我们需要将兄弟节点的左节点设为黑色，将兄弟节点设为红色，然后以兄弟节点进行右旋转，然后更新兄弟节点。然后设置兄弟节点的颜色为右节点的颜色，然后将父节点和兄弟节点的左节点设为黑色，最后进行右旋转。最后将根结点设为黑色。

查找

说了最复杂的添加和删除，我们再来看看查找，这里就简单很多了，具体代码如下：

public V get(Object key) {
    Entry<K,V> p = getEntry(key);
    return (p==null ? null : p.value);
}

final Entry<K,V> getEntry(Object key) {
    // Offload comparator-based version for sake of performance
    if (comparator != null)
        return getEntryUsingComparator(key);
    if (key == null)
        throw new NullPointerException();
    @SuppressWarnings("unchecked")
        Comparable<? super K> k = (Comparable<? super K>) key;
    Entry<K,V> p = root;
    
    // 查找操作的核心逻辑就在这个 while 循环里
    while (p != null) {
        int cmp = k.compareTo(p.key);
        if (cmp < 0)
            p = p.left;
        else if (cmp > 0)
            p = p.right;
        else
            return p;
    }
    return null;
}

这个流程算比较简单了，上面注释标明了，这边就不再解释了。

总结

这边通过代码的形式将红黑树的特点展现出来。可以通过上面描述可见，红黑树并没有那么难…